Rational zeta series
In mathematics, a rational zeta series is the representation of an arbitrary real number in terms of a series consisting of rational numbers and the Riemann zeta function or the Hurwitz zeta function. Specifically, given a real number x, the rational zeta series for x is given by
where 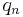 is a rational number, the value m is held fixed, and
is a rational number, the value m is held fixed, and  is the Hurwitz zeta function. It is not hard to show that any real number x can be expanded in this way.
is the Hurwitz zeta function. It is not hard to show that any real number x can be expanded in this way.
Contents |
Elementary series
For integer m, one has
For m=2, a number of interesting numbers have a simple expression as rational zeta series:
and
where γ is the Euler–Mascheroni constant. The series
follows by summing the Gauss–Kuzmin distribution. There are also series for π:
and
being notable because of its fast convergence. This last series follows from the general identity
which in turn follows from the generating function for the Bernoulli numbers
Adamchik and Srivastava give a similar series
A number of additional relationships can be derived from the Taylor series for the polygamma function at z=1, which is
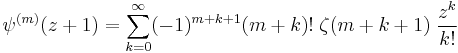 .
.
The above converges for |z|<1. A special case is
which holds for 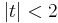 . Here, ψ is the digamma function and
. Here, ψ is the digamma function and  is the polygamma function. Many series involving the binomial coefficient may be derived:
is the polygamma function. Many series involving the binomial coefficient may be derived:
where  is a complex number. The above follows from the series expansion for the Hurwitz zeta
is a complex number. The above follows from the series expansion for the Hurwitz zeta
taken at 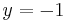 . Similar series may be obtained by simple algebra:
. Similar series may be obtained by simple algebra:
and
and
and
For integer 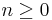 , the series
, the series
can be written as the finite sum
The above follows from the simple recursion relation 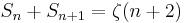 . Next, the series
. Next, the series
may be written as
for integer 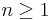 . The above follows from the identity
. The above follows from the identity 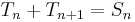 . This process may be applied recursively to obtain finite series for general expressions of the form
. This process may be applied recursively to obtain finite series for general expressions of the form
for positive integers m.
Half-integer power series
Similar series may be obtained by exploring the Hurwitz zeta function at half-integer values. Thus, for example, one has
Expressions in the form of p-series
Adamchik and Srivastava give
and
where 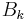 are the Bernoulli numbers and
are the Bernoulli numbers and  are the Stirling numbers of the second kind.
are the Stirling numbers of the second kind.
Other series
Other constants that have notable rational zeta series are:
References
- Jonathan M. Borwein, David M. Bradley, Richard E. Crandall (2000). "Computational Strategies for the Riemann Zeta Function". J. Comp. App. Math. 121: p.11. http://www.maths.ex.ac.uk/~mwatkins/zeta/borwein1.pdf.
- Victor S. Adamchik and H. M. Srivastava (1998). "Some series of the zeta and related functions". Analysis 18: pp. 131–144. http://www-2.cs.cmu.edu/~adamchik/articles/sums/zeta.pdf.

![x=\sum_{n=2}^\infty q_n \left[\zeta(n)- \sum_{k=1}^{m-1} k^{-n}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/dc326fefdb1ff714f1317d1586d36533.png)
![1=\sum_{n=2}^\infty \left[\zeta(n)-1\right]](/2012-wikipedia_en_all_nopic_01_2012/I/a9809620b090aff95cf5870d0cbd53f8.png)
![1-\gamma=\sum_{n=2}^\infty \frac{1}{n}\left[\zeta(n)-1\right]](/2012-wikipedia_en_all_nopic_01_2012/I/b8110c6df07dd108aa09de41cc94ae9b.png)
![\log 2 =\sum_{n=1}^\infty \frac{1}{n}\left[\zeta(2n)-1\right]](/2012-wikipedia_en_all_nopic_01_2012/I/aa16671ba501da97bb2b5c81d6ad613a.png)
![\log \pi =\sum_{n=2}^\infty \frac{2(3/2)^n-3}{n}\left[\zeta(n)-1\right]](/2012-wikipedia_en_all_nopic_01_2012/I/49d6bfacf1f47c6d5419b1a49f167543.png)
![\frac{13}{30} - \frac{\pi}{8} =\sum_{n=1}^\infty \frac{1}{4^{2n}}\left[\zeta(2n)-1\right]](/2012-wikipedia_en_all_nopic_01_2012/I/5ec38e08bb37819a1519afc2bc94628b.png)
![\sum_{n=1}^\infty (-1)^{n} t^{2n} \left[\zeta(2n)-1\right] =
\frac{t^2}{1%2Bt^2} %2B \frac{1-\pi t}{2} - \frac {\pi t}{e^{2\pi t} -1}](/2012-wikipedia_en_all_nopic_01_2012/I/5c05dc349ea17381bfb7c8be41ac56db.png)
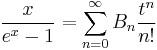
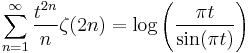
![\sum_{n=2}^\infty t^n \left[\zeta(n)-1\right] =
-t\left[\gamma %2B\psi(1-t) -\frac{t}{1-t}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/6aa5066cf2109dc4b7ce3eb375da2271.png)
![\sum_{k=0}^\infty {k%2B\nu%2B1 \choose k} \left[\zeta(k%2B\nu%2B2)-1\right]
= \zeta(\nu%2B2)](/2012-wikipedia_en_all_nopic_01_2012/I/6083a96c4d16d1a46a9ac8465e362a56.png)

![\sum_{k=0}^\infty {k%2B\nu%2B1 \choose k%2B1} \left[\zeta(k%2B\nu%2B2)-1\right]
= 1](/2012-wikipedia_en_all_nopic_01_2012/I/07a6bdb619a2051c32f6ac4fc353a64a.png)
![\sum_{k=0}^\infty (-1)^k {k%2B\nu%2B1 \choose k%2B1} \left[\zeta(k%2B\nu%2B2)-1\right]
= 2^{-(\nu%2B1)}](/2012-wikipedia_en_all_nopic_01_2012/I/b1e72d52d388a9369c22a7b7b51c963d.png)
![\sum_{k=0}^\infty (-1)^k {k%2B\nu%2B1 \choose k%2B2} \left[\zeta(k%2B\nu%2B2)-1\right]
= \nu \left[\zeta(\nu%2B1)-1\right] - 2^{-\nu}](/2012-wikipedia_en_all_nopic_01_2012/I/efaf0e56b321e849e4cca320a3d902d9.png)
![\sum_{k=0}^\infty (-1)^k {k%2B\nu%2B1 \choose k} \left[\zeta(k%2B\nu%2B2)-1\right]
= \zeta(\nu%2B2)-1 - 2^{-(\nu%2B2)}](/2012-wikipedia_en_all_nopic_01_2012/I/9d0bd4745cc7b60bd342249f675679c8.png)
![S_n = \sum_{k=0}^\infty {k%2Bn \choose k} \left[\zeta(k%2Bn%2B2)-1\right]](/2012-wikipedia_en_all_nopic_01_2012/I/cd4c9ea9e94b683c4479356faaacd392.png)
![S_n=(-1)^n\left[1%2B\sum_{k=1}^n \zeta(k%2B1) \right]](/2012-wikipedia_en_all_nopic_01_2012/I/830a2de515ba4efd339e34ebe707b4ea.png)
![T_n = \sum_{k=0}^\infty {k%2Bn-1 \choose k} \left[\zeta(k%2Bn%2B2)-1\right]](/2012-wikipedia_en_all_nopic_01_2012/I/570a6c491f32ce23187c1f5026d09c59.png)
![T_n=(-1)^{n%2B1}\left[n%2B1-\zeta(2)%2B\sum_{k=1}^{n-1} (-1)^k (n-k) \zeta(k%2B1) \right]](/2012-wikipedia_en_all_nopic_01_2012/I/ad3fcc1408f9bba0ae94d987cb0bdd10.png)
![\sum_{k=0}^\infty {k%2Bn-m \choose k} \left[\zeta(k%2Bn%2B2)-1\right]](/2012-wikipedia_en_all_nopic_01_2012/I/931aaa7f091b210dca114f638a52de48.png)

![\sum_{n=2}^\infty n^m \left[\zeta(n)-1\right] =
1\, %2B
\sum_{k=1}^m k!\; S(m%2B1,k%2B1) \zeta(k%2B1)](/2012-wikipedia_en_all_nopic_01_2012/I/d5eeaccd84a9aac8ebd084d06b0b4340.png)
![\sum_{n=2}^\infty (-1)^n n^m \left[\zeta(n)-1\right] =
-1\, %2B\, \frac {1-2^{m%2B1}}{m%2B1} B_{m%2B1}
\,- \sum_{k=1}^m (-1)^k k!\; S(m%2B1,k%2B1) \zeta(k%2B1)](/2012-wikipedia_en_all_nopic_01_2012/I/9311fc7e6c620658e204cd8e5283e18b.png)